作为一道英文题,我们先解释一下题意:
给你一棵树和它的一个 BFS 序,让你判断这个 BFS 序是否是一个从节点 1 开始的合法 BFS 序。
接下来我们进入正题。
第一眼看到这题时,大部分人都会想到,既然是树,那么它一定是一层一层地向下 BFS。
也就是说,BFS 序中越后出现的节点,它树上的深度肯定是大于它前面的节点的。
于是照这个思想打完后,发现 Wrong Answer 了。
显然这个思路是有反例的,比如下图的情况:
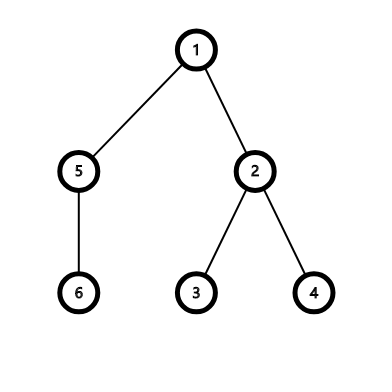
输入给的 BFS 序为:1 5 2 3 4 6
如果根据原来的思路输出就是 Yes,然而正确的 BFS 序显然是 1 5 2 6 3 4
再仔细思考一下,发现合法的 BFS 序不仅要满足刚才的深度条件,而且满足每个节点的父亲在 BFS 序中的位置都要不晚于在它后面出现的节点父亲的位置。
这么看貌似时间复杂度是 O(N2) 的,如何减小复杂度呢?
我们发现一个节点的子树是一个连续的区间,我们直接把每个节点重新编号为它父节点的编号,再把连续相同编号的节点的合并成一个节点即可。合并好以后有一个很好的性质,若输入的序列为合法的 BFS 序,重新编号后的序列元素在原序列中的位置单调递增。这样,时间复杂度就降到了 O(n) 了。
以下为代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define gc c = getchar()
int read(){
int x = 0, f = 1; char gc;
for(; !isdigit(c); gc) if(c == '-') f = -1;
for(; isdigit(c); gc) x = x * 10 + c - '0';
return x * f;
}
#undef gc
const int MAXN = 200005;
int nedge, head[MAXN];
struct Edge {
int to, nxt;
} edge[MAXN * 2];
void add(int x, int y){
edge[++nedge].to = y;
edge[nedge].nxt = head[x];
head[x] = nedge;
}
int d[MAXN], f[MAXN], a[MAXN], b[MAXN], id[MAXN];
void dfs(int k, int fa){
d[k] = d[fa] + 1;
f[k] = fa;
for(int i = head[k]; i; i = edge[i].nxt) {
int u = edge[i].to;
if(u == fa) continue;
dfs(u, k);
}
}
int main(){
int n = read();
for(int i = 1; i < n; i++) {
int x = read(), y = read();
add(x, y); add(y, x);
}
dfs(1, 0);
for(int i = 1; i <= n; i++) a[i] = read();
for(int i = 1; i <= n; i++)
if(d[a[i]] < d[a[i - 1]]) return puts("No"), 0;
for(int i = 1; i <= n; i++) id[a[i]] = i;
for(int i = 1; i <= n; i++) b[i] = f[a[i]];
int len = unique(b + 1, b + n + 1) - b - 1;
for(int i = 1; i <= len; i++)
if(id[b[i]] < id[b[i - 1]]) return puts("No"), 0;
puts("Yes");
}
|




v1.5.2