HWS第六期2023冬令营选拔赛 Writeup

 CTF / HWS
被浏览 次

寒假参加了 HWS 冬令营选拔赛，最近整理文件的时候想着记录一下。

整体比赛难度不大，水了个第十名，主要大佬们都去参加 Real World CTF 了，只有我还在这里摸爬滚打 /(ㄒoㄒ)/~~

MISC

sound from somewhere

听了下音频一眼 SSTV，直接就出了。

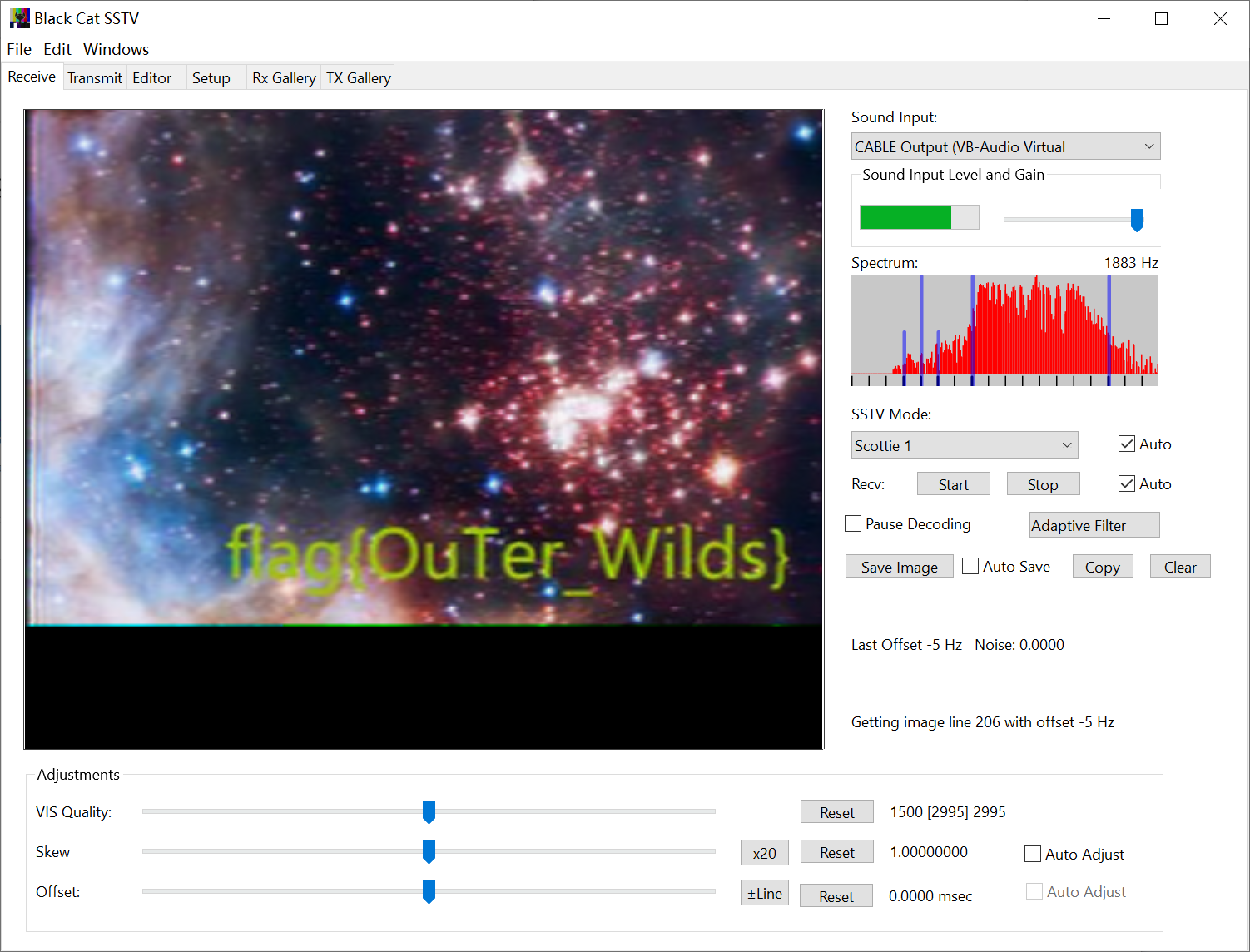
can not speak

比赛的时候都根据教程绕过反调试了，但是还是做不下去。

结果比赛比完和我说有非预期，过反调试就能直接在内存里搜索到 flag？而且比赛出题人复现不出正解，真是服了。

首先 DIE 查一下发现是 VMP 壳，这玩意网上都没啥解决方案，只能尝试过反调试。

以下内容均只为步骤搬运，大部分不了解原理，就看着图一乐吧。

  • 把 PEB 调试位清空：

把 gs:[60] 和 gs:[60]+bc 置零

  • 下软件条件断点：

NtQueryInformationProcess -> rdx == 0x07 || rdx == 0x1E

NtSetInformationThread -> rdx == 0x11

NtQueryInformationProcess 断点命中前一个条件就把 r8 <- 0

运行直至 rdx == 0x1E, 将 r8 <- 0，然后运行到返回，rax <- C0000353

NtSetInformationThread 命中后把 rdx <- 3

  • 禁用软件断点，启用硬件条件断点：

NtClose -> rcx == 0xDEADC0DE

NtQuerySystemInformation -> rcx == 0x23

选择无视异常运行

NtQuerySystemInformation 命中后执行到返回，将 rax <- 0xC0000001

NtClose 命中后将 rcx <- 0

  • 禁用全部断点，运行一次就到用户代码了

或者你直接用 x96dbg 的插件 ScyllaHide，选择 VMP 的 Profile 就行，它原理主要是把上面的一些检测给 nop 了，但是这个代码会检测自身的完整性，在某个函数里会弹窗说文件被篡改，但在这道题里不影响最终效果（

过了反调试运行几次，然后右键 -> 搜索 -> 字符串就能直接看到内存里的 flag 了。

REVERSE

babyre

jadx 打开看了眼，先是有个明显的加密代码，但是感觉没那么简单直接跳过了。

然后发现有个动态加载 dex 文件的代码，又发现有个解密 assets 文件夹下 enc 的代码段。

直接把 enc 解密成 dex，进去发现是一个 AES + BASE64，CyberChef 一下就出了。

P.S. 我其实一开始并不知道这个动态加载 dex 文件是哪里被调用的，后来听讲解才知道是在 AndroidManifest.xml 中定义了 App 启动前的行为。

easyre

IDA 大致看了眼，程序结构比较常规，大概是输入个字符串加密然后和密文比较，然后加密是 TEA 系列的加密，比较用的 memcmp。

直接调试发现中途会直接异常退出，想到刚开始新建了线程，猜测是检测了主进程是否长时间挂起，直接退出。然后 hook 了 NtClose 就过了，就没管具体实现了。

动调的时候在加密函数下断拿到了 key，在 memcmp 下断，得到了密文长度和密文。IDA 里看加密函数的时候第一眼以为改了不少，后来发现类似以下代码

1
2
3
4
5
v8 = v4 + dword_140005728[v6 & 3];
v9 = v4 - 1640531527;
v10 = (v8 ^ (result + ((16 * result) ^ ((unsigned int)result >> 5)))) + v2;
v11 = ((v9 + dword_140005728[(v9 >> 11) & 3]) ^ (v10 + ((16 * v10) ^ (v10 >> 5)))) + result;
v12 = (v9 + dword_140005728[v9 & 3]) ^ (v11 + ((16 * v11) ^ (v11 >> 5)));

其中的 v8 都是没用的，中间那一坨都可以改写成一致的形式，就是个改了 delta 方向和数值的 XTEA。

解密拿到原文包上 flag 就出了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <bits/stdc++.h>
using namespace std;
unsigned enc[] = {0xC0B29B34, 0xEF30AF6A, 0x98CCB238, 0x85B6F195,
                  0xA2480685, 0xA63D9B59, 0xF191C71E, 0x6790767B};
unsigned key[] = {0x29, 0x4823, 0x18BE, 0x6784};
const unsigned delta = 1640531527;
void decode(unsigned &v0, unsigned &v1) {
  unsigned sum = -delta * 32;
  for (int i = 0; i < 32; i++) {
    v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
    sum += delta;
    v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
  }
}
void intToStr(unsigned x) {
  putchar(x & 0xff);
  putchar(x >> 0x8 & 0xff);
  putchar(x >> 0x10 & 0xff);
  putchar(x >> 0x18 & 0xff);
}
int main() {
  for (int i = 0; i < 4; ++i) decode(enc[i << 1], enc[i << 1 | 1]);
  for (unsigned x : enc) intToStr(x);
}

P.S. 看冬令营的讲解发现在主函数之前有一些操作，寒假里有个 KM 推荐学弟做的 bbctf 也有类似的操作，看到时候能不能开个新坑。

repy

这题比赛的时候没做出来，反而最后一部分的脑洞和出题人对上了，有点难绷。

这题一共分为 3 部分，前 2 个部分都用了控制流平坦化，一点一点来吧。

第一部分其实很简单，当时被吓退了，代码其实并不复杂，甚至可以直接手搓。

大致逻辑如下：

1
2
3
4
5
6
7
8
9
10
11
12
bool check(char s[]) {
  int v[10];
  memset(v, 0, sizeof(v));
  for (int i = 0; s[i]; ++i) {
    // ... 省略一些合法性判断，如输入长度为 10 等
    ++v[s[i] - '0'];
  }
  for (int i = 0; i < 10; ++i) {
    if (s[i] - '0' != v[i]) return 0;
  }
  return 1;
}

虽然这个手推是个小学奥数题，但是最近刚学了 z3，正好写个脚本一把梭了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from z3 import *

X = [BitVec(f'X_{i}', 5) for i in range(10)]

check = [X[i] == (1 - ((((X[0] ^ i) & 8) >> 3) | (((X[0] ^ i) & 4) >> 2) | (((X[0] ^ i) & 2) >> 1) | ((X[0] ^ i) & 1))) +
                 (1 - ((((X[1] ^ i) & 8) >> 3) | (((X[1] ^ i) & 4) >> 2) | (((X[1] ^ i) & 2) >> 1) | ((X[1] ^ i) & 1))) +
                 (1 - ((((X[2] ^ i) & 8) >> 3) | (((X[2] ^ i) & 4) >> 2) | (((X[2] ^ i) & 2) >> 1) | ((X[2] ^ i) & 1))) +
                 (1 - ((((X[3] ^ i) & 8) >> 3) | (((X[3] ^ i) & 4) >> 2) | (((X[3] ^ i) & 2) >> 1) | ((X[3] ^ i) & 1))) +
                 (1 - ((((X[4] ^ i) & 8) >> 3) | (((X[4] ^ i) & 4) >> 2) | (((X[4] ^ i) & 2) >> 1) | ((X[4] ^ i) & 1))) +
                 (1 - ((((X[5] ^ i) & 8) >> 3) | (((X[5] ^ i) & 4) >> 2) | (((X[5] ^ i) & 2) >> 1) | ((X[5] ^ i) & 1))) +
                 (1 - ((((X[6] ^ i) & 8) >> 3) | (((X[6] ^ i) & 4) >> 2) | (((X[6] ^ i) & 2) >> 1) | ((X[6] ^ i) & 1))) +
                 (1 - ((((X[7] ^ i) & 8) >> 3) | (((X[7] ^ i) & 4) >> 2) | (((X[7] ^ i) & 2) >> 1) | ((X[7] ^ i) & 1))) +
                 (1 - ((((X[8] ^ i) & 8) >> 3) | (((X[8] ^ i) & 4) >> 2) | (((X[8] ^ i) & 2) >> 1) | ((X[8] ^ i) & 1))) +
                 (1 - ((((X[9] ^ i) & 8) >> 3) | (((X[9] ^ i) & 4) >> 2) | (((X[9] ^ i) & 2) >> 1) | ((X[9] ^ i) & 1)))
          for i in range(10)]

_range = [And(0 <= X[i], X[i] <= 9) for i in range(10)]

s = Solver()
s.add(_range + check)
if s.check() == sat:
     t = s.model()
     res = [t[X[i]].as_long() for i in range(10)]
     print(''.join(str(x) for x in res))
else:
     print(s.check())

得到第一问的输入 6210001000。

紧接着程序根据第一问的答案对内存中的数组进行换表，全是控制流平坦化，用了冬令营的时候推荐的插件 D810 进行求解。

反混淆以后发现程序将第二问输入的字符串和处理后的表一一对应了起来，存到一个数组里，中间有一片代码都没对这个数组进行处理（也可能是 IDA 反编译出错了）。

紧接着直接传进 sub_401600 又通过表还原回输入的字符串，然后对其进行 MD5 并与一段已知值比较，破解可得 yOUar3g0oD@tc4nd。

然后就一头雾水了，比赛后根据讲解，左边还有 sub_402930 等函数不在流程中，其中 sub_402930 调用了文件输入输出，内部还有加密，极有可能和剩下两个文件有关。

中间有很多没啥用的垃圾赋值语句，去掉以后连逆带猜得到这个逻辑：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int __fastcall sub_402930(char *iv, char *key) {
  int i, len_iv = strlen(iv);
  char s[32];
  for (i = 0; i < 16; ++i) {
    s[i + 16] = i < len_iv ? iv[i] : 2;
  }
  for (i = 0; i < 16; ++i) {
    s[i] = key[i];
  }
  char enc[] = "qgapgv,`kl_nbdj`-ejof";
  for (i = 0; i < 10; ++i) {
    enc[i] ^= 2;
    enc[i + 11] ^= 3;
  }
  // enc[] = "secret.bin_magic.file"
  // ... 读取 magic.file，没啥大用
  AES_set_encrypt_key(key, 128, ptr);
  AES_cbc_encrypt(in, out, len, ptr, s + 16, 1LL); // s + 16 是 iv 填充到 16 位
  // ... 写入 secret.bin
}

用脚本将 secret.bin 解密：

1
2
3
4
5
6
7
8
9
10
11
from Crypto.Cipher import AES

enc = open('secret.bin', 'rb').read()

key = b'yOUar3g0oD@tc4nd'
iv = b'6210001000' + b'\x02' * 6
aes = AES.new(key, AES.MODE_CBC, iv)
raw = aes.decrypt(enc)

with open('decrypted.pyc', 'wb') as f:
    f.write(raw)

然后是脑洞部分，根据题目名以及题中字符串 But someone told me that he caught 38 giant snakes yesterday..... （Anaconda 有蟒蛇的意思，还告诉了版本是 3.8），或者直接拿 DIE 检测都能知道它是 Python 3.8 的文件。

用 3.8 版本的 python 反汇编字节码发现会报错，检查报错信息发现它通过 JUMP_FORWARD 36 来跳过非法的字节码，同时影响反汇编。

通过 dis.opmap 我们得知 JUMP_FORWARD 36 的字节码为 6E 24，NOP 的字节码为 09。

1
2
3
4
5
6
7
8
9
10
11
# 注意要 3.8 版本的 python
import dis, marshal

for op, opcode in dis.opmap.items():
    print(f'{op}:{opcode}')
print('-----------------------------')

f = open('decrypted.pyc', 'rb')
code = f.read()
code = marshal.loads(code[16:])
print(dis.dis(code))

于是我们可以 patch 字节码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
with open('decrypted.pyc', 'rb') as f:
    code = bytearray(f.read())
    op_len = len(code)
    for i in range(op_len):
        if code[i] == 0x6E and code[i + 1] == 0x24:
            i += 2
            nop = 0x24
            while nop > 0:
                code[i] = 0x09
                nop -= 1
                i += 1

with open('patched.pyc', 'wb') as f:
    f.write(bytes(code))

然而还是有部分代码无法复原，而且部分 while 有关控制流反编译是错误的，只能去自己阅读字节码。

主函数和之前程序一样只会连逆带猜，总感觉哪里少了点啥，能猜出有个 try 语句块异常处理来让前半段异或上后半段，但是整不出完整的逻辑，因为字节码顺序变得很奇怪，就和前面的 sub_402930 是怎么被调用的一样莫名其妙。

然后再说会能被直接反编译的三个类：

  • II00O0III0o0o0o0oo 类是一个换表 BASE64
  • IIoo00IIIo0o0oo0oo 类是一个 TEA 系列的加密
  • chall 类先调用了 II00O0III0o0o0o0oo 类，然后调用 IIoo00IIIo0o0oo0oo 类

也就是说加密逻辑是先换表 BASE64 然后 TEA 系列加密，这样我们就可以开始写脚本了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
from string import ascii_uppercase, ascii_lowercase, digits
from ctypes import c_uint
import base64

class b64:

    def __init__(self):
        self.std_table = ascii_uppercase + ascii_lowercase + digits + '+/'
        self.custom_table = list(self.std_table)
        length = len(self.custom_table)
        for i in range(0, length // 2):
            for j in range(0, length - 1 - i):
                if self.custom_table[j] > self.custom_table[j + 1]:
                    temp = self.custom_table[j]
                    self.custom_table[j] = self.custom_table[j + 1]
                    self.custom_table[j + 1] = temp
        self.custom_table = ''.join(self.custom_table)
        self.strmap = bytes.maketrans(self.custom_table.encode(), self.std_table.encode())

    def b64decode(self, enc):
        return base64.b64decode(enc.translate(self.strmap)).decode()

class TEA:
    
    def __init__(self):
        self.d = 0x87654321
        k0 = 1732584193
        k1 = 0xEFCDAB89
        k2 = 0x98BADCFE
        k3 = 271733878
        self.k = [k0, k1, k2, k3]

    def TEAdecode(self, v):

        def MX(x, y, total, key, p, e):
            a = (x.value >> 6 ^ y.value << 4) + (y.value >> 2 ^ x.value << 5)
            b = (total.value ^ y.value) + (key[p & 3 ^ e.value] ^ x.value)
            return c_uint(a ^ b)

        n = len(v)
        key = self.k
        delta = self.d
        rounds = 6 + 52 // n
        total = c_uint(delta * rounds)
        e = c_uint(0)
        for i in range(rounds):
            e.value = total.value >> 2 & 3
            v[n - 1] = c_uint(v[n - 1] - MX(c_uint(v[n - 2]), c_uint(v[0]), total, key, n - 1, e).value).value
            for p in range(n - 2, 0, -1):
                v[p] = c_uint(v[p] - MX(c_uint(v[p - 1]), c_uint(v[p + 1]), total, key, p, e).value).value
            v[0] = c_uint(v[0] - MX(c_uint(v[n - 1]), c_uint(v[1]), total, key, 0, e).value).value
            total.value -= delta
        return v

class solver:

    def __init__(self):
        self.b64 = b64()
        self.TEA = TEA()
    
    def ints2bytes(self, v):
        n = len(v)
        res = b''
        for i in range(n // 2):
            res += int.to_bytes(v[2 * i], 4, 'little')
            res += int.to_bytes(v[2 * i + 1], 4, 'little')
        return res

    def bytes2ints(self, cs):
        new_length = len(cs) + (8 - len(cs) % 8) % 8
        barray = cs.ljust(new_length, b'\x00')
        i = 0
        v = []
        while i < new_length:
            v0 = int.from_bytes(barray[i:i + 4], 'little')
            v1 = int.from_bytes(barray[i + 4:i + 8], 'little')
            v.append(v0)
            v.append(v1)
            i += 8
        return v
    
    def decode(self, text):
        tmp = self.TEA.TEAdecode(self.bytes2ints(text))
        return self.b64.b64decode(self.ints2bytes(tmp))

with open('encrypted', 'rb') as f:
    sol = solver()
    enc = bytearray(f.read())
    part_1 = enc[:len(enc) // 2]
    part_2 = enc[len(enc) // 2:]
    for i in range(len(enc) // 2):
        part_1[i] ^= part_2[i]
    print(sol.decode(part_1))

解出最后一部分是 PytH0n_KZBxDwfkIzbEgUOY，把三部分按题目要求合起来就是 flag。

CRYPTO

Numbers Game

发现有随机过程生成了两个长度为 53 的序列，算了下 (128 + 256) / 32 * 52 = 624，正好能满足解出随机数盒的条件。getrandbits 內部实现是反复生成 32 bits 的数，从 LSB 填充到 MSB，多余的 bits 就 drop。正好 128 和 256 都是 32 的倍数，可以完全复原生成的 32 bits 的数。 最后就只要倒推之前的生成的两个数即可。

逆推 state 盒的参考资料：https://badmonkey.site/archives/mt19937.html#2020-vn-招新赛-backtrace

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
import hashlib
import random

_id = ['d5d97afad7ef619b4badd8d2da10ee24', '67f4660a8335fb9f4152a9fbc44c9c77', '8cd43c85ebe9cc7036a37f47ccd1d1e4', 'ee3e8c62e8b0100027589d6de82677ef', '463bb2f3731ad0e786302bf78da08330', 'e245b1852a3b92734e46eb3421bd76c9', '0b74736786b4ab94651e3b706a548e55', '79cb596b28c2b4e02738f93b5bfbe0d3', '5a9c46837952952045564b5b395acad1', 'd3c2d90a05d1a059fbeba4a05a608798', '4da0306c8ab58097d2fef9114e6fcb6d', '9707fabbd3c96de66917f15998ac9201', '9dd3e46fc930abfb523fe31e8ee8a658', '3716a8fd05f7388e7151d09431e61ee1', '9acf027679a6d7a674a43dee4f5bea35', '78702a2b125a940519337b1bf50aff8a', '262cf3b8c8072a602048a24756c83fcf', '092f8d227ec583c4734a6f449de521a3', '712aa300302b57fed458553426348fce', '834d4a0ea451cc04b469636b18c56435', '754b5284b14402c61e3b1e56cb2d41e9', '51d742ca6a341032afcb5dc645f54bfa', 'c1a33d104f47e33d6932905b483a2018', '3def7c2a14cff6b2864a2100956df07f', '7e3606e4ec1c99fe5a8593ae44f25a70', '404c6139570883dbab8e5a299d7a5017', 'f07597079e1b68ebb4e2d16b83b7b484', '0723daf5c65f8ba6cd6e43fcdf9d18dc', '4c54db12829f165837384b66978e8438', 'cd056e64e1f31461cab2e66ece9d3278', '2f6ae16fab122cbce240e32464a1ab57', 'f86e0e9ee23498340f62d8617f6f5218', 'af4ebe2535885c783c89f8d8c4815076', 'c8eae5b5c7aca2c5fdb4f284e2cf65c5', 'bec0d8ecabedd9811a8ecb6052b21d8c', '731bd3421b6517aa101357fe1c49caf3', '344f4a26cdaf1a782d9b32208e1a3e92', '892b1741d304878461dd0774a335ea3d', '56e2a484ca40f43e059bf5f0bd822bdc', 'd7c0762df71b31c14654147fb9a0595c', '57016a179ba5509f6b04a161ac628b34', 'e49a2d573522c1ee3e8348ceca0295a4', '4b0f49c7e6469e82832e9cc90b9e17c0', 'eadc9d0c8b75127fe0a7f71881de1ea7', 'db9fe5537768207bd8cdf770bcd42dfa', 'ba2f57578752628d1ecac419b3a8bc36', '3752e70b5d2b578a8d412d84aab43705', '54e97795df8781c776cbb1ce4f5f31fc', '32794880abc9f68102c24e92ad9c7cd5', 
'b5eb7e651ca298f6873694c47d1cd3da', 'a188934777d2c67e3d59692135005497', '34c308fa1644b387169ea88c1b575490']
_code = ['2eebed894580fb900c3615d4866150e68322ff4d48e7509f85ff4543969b0cf6', '017aefd63b4ce14eb376161902d92894a15f680e7b055ce25c3b02c6b49db0a6', 'e12d945904032887c967ae03a48c8b096abc79dc64134d872693599d4f6c91cc', '0f8957f365f53a7209baa852905c5da5dba54ddb403ab17a4c9b3a051540d49c', '091e3e41815cd32f482f2cf54ac3338fc918c2a657896af1aa1b23ea528664f4', '5916cd18e8c48c545232112f2179aa7a722350a8a0ced4f1363cc61bc9d83630', '37702710d47a1c17278743253123f6eac85b16d9393432ec65100143bc8657e8', 'c3a7006293c48957cba5c010f945483cfdc47650a79d0e8a8a9a52c174244a10', 'e1a90a475dd21da64d64ea1dd50a82a622061d08e9d4b3016982c4a0b42f1251', '2f40ff85024765e58ed175927c53e0a279cda96ce755b602f89bfc171108ba3d', 'f4f8337dd7267d02638a9cc531c8a02fe0316dd5ff6f8c8aec898c060c6fb217', '0df2f3fe1eb976944a2de5729fca4a12b83c8329b4f514869856ebb94b7d7bf9', 'abb2f1277b1cb5ad07254b7f7ed346bcdb73282b306123ce0b5befe42a9e796d', '6ef31ed6a2a465bcd146c2438bf391bfd9f3187cf54afae512220a7a94714bf3', '6981f99ba288923a5cd68908ecc8795bf301f1e7d081ac6580a63902fd52da01', 'b6b07975697de1c0342e3711b59165b849125794ef2541c6c60dcf40e689df7b', '20e3af3a2bcedfd15199975cc9edcde14cb13fdff3ea0607a4747601e500aede', '606aa1daf188b9dd5fd6141312f1828846f92baa519e70e5c6923a352421fe2f', '1dc6a60112e99c5b884c0bb5430a7a54eba8aef34fada9cb96bce79a22456cf2', 'fd81e36f576119a19185cd12e87544b42f9fcc3dcb5e7ba282b1a128d73d63c5', '7a01e947ca012a5c9a8dd20e693a7788cd6157a5c3fce5fa7c7e09014ea3266e', 'ccd162b182c773062514ffc3551ed47f32293700083782d902efc55b1e9795c6', 'dbb6115aefd2638eebf44d3be6e9525e09ff036269d954469a0f925b496327a7', 'ac08696fe64bb5e58cd3e558463213ca08ab7805e33f45459ae14b35fc5858c6', '6e1594596ad1c656635af29d14b22a5ed10e545442eea5f4e056e20d11aa33b3', '4afd17e64562603c66ce0ca42d544ca48511c3d560f9180c231a9ccb28a0e55e', '06b2d2b24ca626e18fdcb3196e989e3b05150500815511f48200ddea9aacda48', '947a11e8258fd161d02b0eb1b2e8fcd9ff1684a7c75f7c506ddee91f08316f56', 'a0e58b15736cab055be1d03860dedb6b8136f6739308c2e0ef6a7490c6b4a1f1', '31476f64f96d72a398e7eb789068b8cfd61ed9cac95d76824a2bbf5b682ea72d', '974259198846a4849d318afd325d860a6e40dfd39e1ed8c7b6d87c990e35efcf', 'e93d02ba7079c488c30e377794b4fcc62eeafb6c3f02197f1ebc059e3e5f7f07', 'ded96eec0d25c05a54671a001bcd99f5c6d3991d2fdf80afb8f0861a44f3fd64', '86f34c1da65f07634de7c302a6df306dd545806022411a318900bd33b0aff9bd', '59baf4cf3d3b85fcdefd1a9b60c3d78926ff73650ac375c616b30fe9063b377d', '02f2ee251ecc19fa52dd42c0e0b609bc2e7a8ae11ce6ca35396a4bc74d12ac63', '597d09b4c43012b1b4b040d8c62d5fb02d1c4249de4eea06e1447000ba53f50c', 'bb87bd8e1903db2df41c349914e9f3591bb032400be6e86ed10e7d292243a374', 'cec38960069fdc8090cfbdd166e15ec8a77ce5b4d6b350805a63d2b54cbf0187', '1439d35a9c0caa9cacabe8e6179a02d51ebb9fb51125d5eeaba47ff6b8abcc97', '820d72d49e0fd86ef47b022a3091b326be8b0d2a42f87cbc918737b9972ea62f', 'e625e82100031fa4a4410700034859cd4b35c086f5ac2870c6909c16a6831bfc', 'f0e22f5167d29331351e1718c17b5420f6a29d84357273e1bfb24c2ff34fa675', 'a5a7991f0c5c6a44f68c5c18661611057dbabeff7847623315ce784095645f75', '07cd3f5c5c690214af5feda27b3aec257543a8f96bc509805028a0e95c5d98c6', 
'6e5dd4405c1b446b9530e4d9356c05b71d1bfcf8a79778588143c3b6fec3fded', 'a33f821d277e6f73c09a5ecd14cef80bac29ffe2b917225c27725d2447ac0489', 'c18a4a02dd1f7ee65bf5596c53549c286a754afb0e3b90b2369cdd1e43c0b986', '6b8df66aa27b40ca275bc133958b5d543167edf919e7e623a496c9afbf7594d6', 'c48124eeef995c7bb705bd240a26dbf6bdbe42ba29addf7ac78fa28dbed3debe', '040eef11dc6e0f3bb3e58e12d2a57ee274071a9c6224f27db70e19a8aa7d4df2', '4ecd0a955e52657fab8dfdac2df4d805f1d08b031df8bce22ac01fe20ca72c5b']

# right shift inverse
def inverse_right(res, shift, bits = 32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift
    return tmp
# right shift with mask inverse
def inverse_right_values(res, shift, mask, bits = 32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift & mask
    return tmp
# left shift inverse
def inverse_left(res, shift, bits = 32):
    tmp = res
    for i in range(bits//shift):
        tmp = res ^ tmp << shift
    return tmp
# left shift with mask inverse
def inverse_left_values(res, shift, mask, bits = 32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp << shift & mask
    return tmp

def recover_state(out):
    state = []
    for i in out:
        i = inverse_right(i, 18)
        i = inverse_left_values(i, 15, 0xefc60000)
        i = inverse_left_values(i, 7, 0x9d2c5680)
        i = inverse_right(i, 11)
        state.append(i)
    return state

def backtrace(cur, num):
    high = 0x80000000
    low = 0x7fffffff
    mask = 0x9908b0df
    state = cur
    for i in range(num - 1, -1, -1):
        tmp = state[i + 624] ^ state[i + 397]
        if tmp & high == high:
            tmp ^= mask
            tmp <<= 1
            tmp |= 1
        else:
            tmp <<= 1
        res = tmp & high
        tmp = state[i - 1 + 624] ^ state[i + 396]
        if tmp & high == high:
            tmp ^= mask
            tmp <<= 1
            tmp |= 1
        else:
            tmp <<= 1
        res |= (tmp) & low
        state[i] = res    
    return state

def hex2bin(x, bits):
    return bin(int(x, 16))[2:].zfill(bits)

def getRndHex(rnd, bits):
    return hex(prng.getrandbits(bits))[2:].zfill(bits // 4)

n = len(_id)
num = []

for i in range(n):
    x = hex2bin(_id[i], 128)
    y = hex2bin(_code[i], 256)
    for p in range(3, -1, -1):
        num.append(int(x[p * 32:(p + 1) * 32], 2))
    for p in range(7, -1, -1):
        num.append(int(y[p * 32:(p + 1) * 32], 2))

partS = recover_state(num)
pre = backtrace([0] * 12 + partS, 12)[:624]
prng = random.Random()
prng.setstate((3, tuple(pre + [0]), None))
pre_id = getRndHex(prng, 128)
pre_code = getRndHex(prng, 256)
flag = hashlib.md5((pre_id + pre_code).encode()).hexdigest()
print('flag{%s}' % flag)

# flag{22b307a4ac14c89888d5a6c79f7f963c}

math

看 chal.py，发现主要由 3 部分构成：

  • 读取满足 a2−D×b2=1a^2 - D \times b^2 = 1 的 aa 和 bb

  • 同余

  • 打乱 bits

a2−D×b2=1a^2 - D \times b^2 = 1 是经典的 PELL 方程，可以用连分数得到最小解，然后递推生成通解。

同余过程太经典了，可以直接通过 aa 在 pp 下的逆元和 bb 求出 mm。

还有个打乱，一开始以为和上一道题一样要去看 getPrime 的源码，想想不太实际。

注意到 mm 肯定是小于 pp 的（不然不用解了），pp 只有 512 bits，85 bits 一个组，最多也就 6 组（事实上题目已经给了 cc）。

直接全排列枚举复杂度才 6! = 720 完全可以接受，枚举 aa, bb 通解，枚举全排列，求解 mm 看是否为 b'flag' 开头。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import itertools
from gmpy2 import *
from Crypto.Util.number import *

def sol_PELL(D):
    m = isqrt(D)
    x = D**(0.5)
    num=[]
    num.append(m)
    b = m
    c = 1
    while num[-1] != 2 * num[0]:
        c = (D - b**2) // c
        tmp = (x + b) // c
        num.append(int(tmp))
        b = num[-1] * c - b
    num = num[:-1]
    num.reverse()
    x, y = 1, 0
    for i in num:
        y, x = x, i * x + y
    return x, y

D = 0x1337
a0, b0 = sol_PELL(D)

p = 11199186558148426014734492874345932099384932524559726349180064588241518696390926354448476750322781683505497782040786332571272422812867731614415519029276349
plist = ['0010101111100011101101011111111001011000100110001001000000010001111011110101110011111', '0011010010010010110010011011001100110001100010101110001010001101110001100000111011010', '0110101101011101110000100001000000010001110110001010000000010110010101100100101110000', '0100111001011010000101100111100110101100011100100111011000110001111101000110110101101', '1100100110011101010011011111000101011011010000101100011001110100101000101101111110100', '1110111110001110000101100000000100111010110000001111010001101001100001010110101010001']

def work(a, b):
    inv = invert(a, p)
    perms = list(itertools.permutations(plist))
    for perm in perms:
        s = ''
        for _ in perm:
            s = s + _
        num = int(s, 2) % p
        m = ((num - b) % p + p) % p
        m = m * inv % p
        assert(num == (a * m + b) % p)
        flag = long_to_bytes(m)
        if (flag[:4] == b'flag'):
            print(flag)
            return True
    return False

a, b = a0, b0
while not work(a, b):
    a, b = a * a0 + D * b * b0, a * b0 + b * a0
    assert(a**2 - D * b**2 == 1)
    
# b'flag{5b80aaa2-2bb2-0ef1-4aa0-a5a9387239d5}'
 上一页